PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU
Nama : Syalsa Sabina Zahwa (29)
Kelas : X MIPA 1
PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU
Setelah memahami ukuran sudut yaitu derajat dan radian, selanjutnya yang harus kita pahami dalam konsep trigonometri yaitu sinus, cosinus, tangen, cosecan, secan, dan cotangen pada segitiga siku-siku.
Trigonometri sangat erat kaitannya dengan sudut segitiga, karena asal kata trigonometri sendiri yang berarti mengukur tiga sudut (berasal dari kata Yunani, trigonon: tiga sudut dan metro: mengukur). Jika berbicara mengenai trigonometri tidak akan bisa lepas dari sinus, cosinus, tangen, cosecan, secan, dan cotangen.
Perbandingan Trigonometri dari Suatu Sudut pada Segitiga Siku-Siku
Segitiga siku-siku yaitu segitiga dengan salah satu sudutnya adalah 90°. Dalam segitiga siku-siku terdapat sisi miring yang disebut hipotenusa. Kuadrat hipotenusa yaitu jumlah dari kuadrat dua sisi lainnya. Secara sistematis, teorema Pythagoras dapat dinyatakan sebagai berikut.
dengan a dan b adalah sisi siku-siku dan c adalah sisi miringnya. Untuk lebih jelasnya maka perhatikan gambar berikut :
Perbandingan Sinus (sin), Cosinus (cos), Tangen (tan), Cosecan (scs), Secan (sec), dan Cotangen (cot).
Diberikan segitiga ABC siku-siku di B dengan ∠ A = θ.
Jika sisi di depan sudut (opposite) dinamakan "depan", sisi di samping sudut (adjacent) dinamakan "samping" dan sisi miring (hypotenuse) dinamakan "miring", maka perbandingan sisi-sisi tersebut didefinisikan sebagai berikut :
Cosecan adalah kebalikan dari sinus, ditulis
Untuk mengetahui rasio trigonometri, kita menggunakan segitiga siku-siku. Untuk itu, kita harus mengetahui letak sisi depan, sisi samping, dan sisi miring. Untuk lebih jelasnya perhatikan gambar berikut :
• Sisi Miring adalah sisi di depan sudut siku-siku.
• Sisi Depan adalah sisi di depan sudut α.
• Sisi Samping adalah sisi siku-siku lainnya.
Setelah mengetahui sisi miring, sisi depan, dan sisi samping, selanjutnya kita akan membahas definisi sinus, cosinus, tangen, cosecan, secan, dan cotangen.
Contoh:
Tentukan nilai sinus, cosinus, dan tangen untuk sudut Q dan R pada segitaga berikut.
Jawab :
Contoh Soal :
1. Perhatikan gambar dibawah ini!
Berdasarkan gambar di atas, tentukan besar sudut yang sesuai?
Jawab :
Pembentukan sudut di atas pada umumnya searah jarum jam. Untuk itu tanda sudutnya negatif, maka besarnya -45°. Satu putaran penuh pada umumnya memiliki besar sudut 360º. Untuk itu besar sudut yang sesuai yaitu:
360º – 45º = 315º
Jadi besar sudut yang sesuai adalah 315º.
2. Besar sudut ½ π rad sama dengan . . . º.
Jawab :
Contoh soal perbandingan trigonometri di atas dapat diselesaikan dengan memperhatikan ketentuan bahwa π rad memiliki besar sudut sama dengan 180º. Maka:
½ π rad = ½ x 180º = 90º
Jadi besar sudut ½ π rad sama dengan 90º.
3. Besar sudut 75º sama dengan . . . rad.
Jawab :
Untuk menyelesaikan soal di atas perlu anda ketahui bahwa 1º = π/180 rad. Sehingga:
75º = π/180 rad
= 75 x π/180 rad
= 5/12 π rad
Jadi besar sudut 75º sama dengan 5/12 π rad.
4. Perhatikan gambar di bawah ini!
Gambar di atas terdapat segitiga yang siku sikunya di A. Perbandingan sinus, cosinus, dan tangen pada sudut α dan β tersebut yaitu . . .
Jawab :
Contoh soal perbandingan trigonometri pada segitiga siku siku di atas dapat dinyatakan dalam bentuk persamaan sinus, cosinus dan tangan dalam sudut α dan β. Adapun persamaan perbandingan trigonometrinya yaitu sebagai berikut :
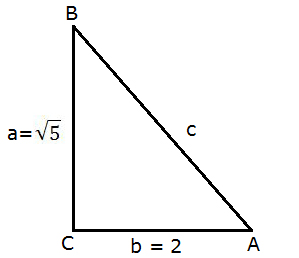
5. Perhatikan gambar di bawah ini!
Tentukan nilai cos α dari segitiga di atas?
Jawab :
Langkah pertama yang harus dilakukan ialah mencari nilai c pada segitiga di atas dapat dilakukan menggunakan teorema phytagoras. Adapun cara mencari nilai c yaitu:
c = √a² + √b²
= √(√5)² + √2²
= √5 + √4
c = √9 = 3
Cos sudut ialah perbandingan sisi samping dengan sisi miring pada segitiga siku siku. Maka hasilnya:
cos α = b/c = 2/3
Jadi cos α dari segitiga di atas ialah 2/3












Komentar
Posting Komentar