SOAL FUNGSI : KUADRAT, RASIONAL, IRASIONAL
Nama : Syalsa Sabina Zahwa (29)
Kelas : X MIPA 1
•》Contoh Soal Fungsi Kuadrat
1.) Persamaan fungsi kuadrat yang grafiknya melalui titik (1, 7), (2, 6), dan (-2, -2) adalah:
a. y = 2×2 + x + 6
b. y = 2×2 – x + 6
c. y = x2 + 2x + 6
d. y = -x2 + 2x + 6
e. y = -x2 – 2x + 6
Jawab: d. y = -x2 + 2x + 6
Pembahasan:
y = ax2 + bx + c
melalui titik (1, 7), maka:
7 = a + b + c …………(i)
Melalui titik (2, 6) maka:
6 = 4a + 2b + c …………(ii)
Melalui titik (-2,-2) maka:
-2 = 4a – 2b + c …………(iii)
Dari (i) dan (ii) diperoleh
a + b + c = 7 |x4| 4a + 4b + 4c = 28
4a – 2b + c = 6 |x4| 4a + 2b + c = 6 –
2b + 3c = 22 (iv)
Dari (ii) dan (iii) diperoleh
4a + 2b + c = 6
4a – 2b + c = -2 –
4b = 8
b = 2
b = 2 di subtitusikan ke (iv) :
2b + 3c = 22
2.2 + 3c = 22
c = 18
c = 6
b = 2 dan c = 6 di subtitusikan ke (i)
a + b + c = 7
a + 2 + 6 = 7
a = -1
jadi persamaan fungsi kuadrat yang di maksud adalah y = -x2 + 2x + 6 (D)
2.) Suatu fungsi kuadrat mempunyai nilai minimum –2 untuk x = 3 dan untuk x = 0, nilai fungsi itu 16. Fungsi kuadrat itu adalah:
a. f(x) = x2 – 6x + 8
b. f(x) = x2 + 6x + 8
c. f(x) = 2×2 – 12x – 16
d. f(x) = 2×2 – 12x + 16
e. f(x) = 2×2 + 12x + 16
Jawab: d. f(x) = 2×2 – 12x + 16
Pembahasan:
Puncak titik (3, -2), maka:
y = a(x – xp)2 + yp
= a(x – 3)2 – 2
Melalui titik (0, 16), maka:
y = a(x – 3)2 – 2
16 = a(0 – 3)2 – 2
18 = 9a
a = 2
jadi persamaan fungsi kuadratnya adalah:
y = 2(x – 3)2 –2
y = 2×2 – 12x + 16 (D)
3.) Persamaan fungsi kuadrat yang memotong sumbu X di titik (-2, 0) dan (2, 0), serta melalui titik (0, 4) adalah:
a. y = 4 – x2
b. y = 4 + x2
c. y = x2 – 4
d. y = 2×2 – 4
e. y = 4 – 2×2
jawab: a. y = 4 – x2
Pembahasan:
Memotong sumbu X di titik (-2, 0) dan (2, 0) maka:
y = a(x – x1)(x – x2)
= a(x – (-2))(x – 2)
= a(x + 2)(x – 2)
Melalui titik (0, 4), maka:
4 = a(0 + 2)(0 -2)
4 = a(2)(-2)
a = -1
jadi persamaan fungsi kuadratnya adalah:
y = -1(x + 2)(x – 2)
= 4 – x2 (A)
4.) Grafik fungsi kuadrat yang memotong sumbu X di titik (-4, 0) dan (3, 0) serta memotong sumbu Y di titik (0, -12) mempunyai persamaan :
a. y = x2 – x – 12
b. y = x2 + x – 12
c. y = x2 + 7x – 12
d. y = x2 – 7x – 12
e. y = -x2 + 7x – 12
Jawab: b. y = x2 + x – 12
Pembahasan:
Grafik fungsi kuadrat memotong sumbu X di titik (-4, 0) dan (3, 0) maka:
y = a(x – x1)(x – x2)
= a(x + 4)(x – 3)
Memotong sumbu Y di titik (0, -12) maka:
y = a(x + 4)(x – 3)
– 12 = a(0 + 4)(0 – 3)
a = 1
jadi persamaan fungsi kuadratnya adalah:
y = a(x +4)(x – 3)
= 1(x + 4)(x – 3)
= x2 – 3x + 4x – 12
= x2 + x – 12
5.) Grafik fungsi kuadrat yang mempunyai titik balik (1, -4) dan melalui titik (2, -3) persamaan adalah ….
a. y = 2×2 – 2x – 12
b. y = 2×2 – x – 5
c. y = x2 – 2x – 4
d. y = x2 2x – 3
e. y = x2 + 2x – 7
f. jawab: d. y = x2 2x – 3
pembahasan:
titik balik grafik fungsi kuadrat (2, -4) maka;
y = a(x – p)2 + q
= a(x – 1)2 – 4
Melalui titik (2, -3) maka:
Y = a(x – 1)2 -3
-3 =a(2 – 1)2 -4
a = 1
jadi, persamaan fungsi kuadratnya adalah:
y = a(x – )2-4
= 1(x – 1)2-4
=x2 – 2x + 1-4
=x2 – 2x -3
•》 Contoh Soal Fungsi Irasional
1.) Tentukan himpunan penyelesaian dari,










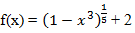
Komentar
Posting Komentar