SOAL KOMPOSISI FUNGSI DAN INVERS FUNGSI
Nama : Syalsa Sabina Zahwa (29)
Kelas : X MIPA 1
Soal Komposisi Fungsi
1). Diketahui: Dua buah fungsi f(x) = 2x - 5 dan fungsi g(x) = x - 3. Tentukan nilai fungsi komposisi (f o g)(x)!
Jawab:
(f o g)(x)= f(g(x)) ->sisipkan fungsi g(x) ke f(x)
= f(x - 3) ->subtitusi g(x) ke f(x)
= 2(x - 3) - 5 ->hitung hasilnya
= 2x - 6 - 5
= 2x - 11
Jadi nilai (f o g)(x) = 2x - 11
2.) Diketahui: Dua buah fungsi f(x) = 3x + 7 dan fungsi g(x) = x - 3. Tentukan nilai fungsi komposisi (g o f)(x)!
Jawab:
(g o f)(x) = g(f(x)) ->sisipkan fungsi f(x) ke g(x)
= g(3x + 7) ->subtitusi f(x) ke g(x)
= 1(3x + 7) - 3 ->hitung hasilnya
= 3x + 7 - 3
= 3x + 4
Jadi nilai(g o f)(x) = 3x + 4
3.) Diketahui:Dua buah fungsi f(x) = 5x - 2 dan fungsi komposisi (f o g)(x) = 10x - 17. Tentukan nilai fungsi g(x)!
Jawab:
(f o g)(x) = 10x - 17 ->cari persamaan nya
f(g(x)) = 10x - 17
5(g(x)) - 2 = 10x - 17 ->subtitusi g(x) ke f(x)
5(g(x)) = 10x - 17 + 2 ->hitung
5(g(x)) = 10x - 15 ->sederhanakan bagi 5
g(x) = 2x - 3
Jadi nilai g(x) = 2x - 3
4.) Diketahui: Dua buah fungsi f(x) = 2x - 5 dan fungsi komposisi (f o g)(x) = 6x + 19. Tentukan nilai fungsi g(x)!
Jawab:
(f o g)(x) = 6x + 19 ->cari persamaan nya
f(g(x)) = 6x + 19
2(g(x)) - 5 = 6x + 19 ->subtitusi g(x) ke f(x)
2(g(x)) = 10x + 19 + 5 ->hitung
2(g(x)) = 10x + 24 ->sederhanakan bagi 2
g(x) = 5x + 12
Jadi nilai g(x) = 5x + 12
5.) Diketahui:Dua buah fungsi g(x) = x - 4 dan fungsi komposisi (f o g)(x) = 4x - 11. Tentukan nilai fungsi f(x)!
Jawab:
(f o g)(x) = 4x - 11
f(g(x)) = 4x - 11
f(x - 4) = 4x - 11
》Misal x - 4 = y maka x = y + 4
f(y) = 4 (y + 4) - 11 ->ubah ke dalam bentuk y
f(y) = 4y + 16 - 11 ->hitung
f(y) = 4y + 5 ->ganti y menjadi x
f(x) = 4x + 5
Jadi nilai f(x) = 4x + 5
Soal Invers Fungsi
》Pembahasan :
Jawabannya : D


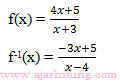
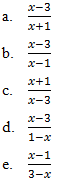

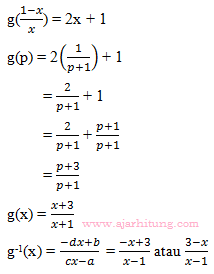


Komentar
Posting Komentar