FUNGSI: KUADRAT, RASIONAL, IRASIONAL
Nama : Syalsa Sabina Zahwa (29)
Kelas : X MIPA 1
•> Fungsi Kuadrat dengan Tabel, Persamaan, dan Grafik
Misal kita punya fungsi kuadrat y = x² dan ingin menggambar fungsi tersebut, kita akan membuat tabelnya terlebih dahulu.
Kita ambil contoh nilai-nilainya seperti pada contoh di bawah ini. Kemudian, tandai titik-titik potongnya dan kita dapati grafik fungsi kuadratnya.
Misal kita punya fungsi kuadrat y = x² dan ingin menggambar fungsi tersebut, kita akan membuat tabelnya terlebih dahulu.
Kita ambil contoh nilai-nilainya seperti pada contoh di bawah ini. Kemudian, tandai titik-titik potongnya dan kita dapati grafik fungsi kuadratnya. Misal kita punya fungsi kuadrat y = x² dan ingin menggambar fungsi tersebut, kita akan membuat tabelnya terlebih dahulu.
L⁹Kita ambil contoh nilai-nilainya seperti pada contoh di bawah ini. Kemudian, tandai titik-titik potongnya dan kita dapati grafik fungsi kuadratnya. Misal kita punya fungsi kuadrat y = x² dan ingin menggambar fungsi tersebut, kita akan membuat tabelnya terlebih dahulu.
Kita ambil contoh nilai-nilainya seperti pada contoh di bawah ini. Kemudian, tandai titik-titik potongnya dan kita dapati grafik fungsi kuadratnya. garis pada grafik tidak boleh tegak lurus karena akan membedakan nilai-nilai yang memenuhinya.
Sebelumnya kita sudah lihat grafik berdasarkan tabel, sekarang kita akan melihat grafik dari persamaan. Persamaan akan memudahkan menggambar titik potong x dan y.
Misalnya kita punya persamaan y = x² + 2x +1, kita cari titik potong terhadap sumbunya.
Titik potong terhadap sumbu y
x = 0
y = 0² + 2(0) +1
y = 1
Titik potong (0, 1)
Titik potong terhadap sumbu x
x² + 2x +1 = 0
(x + 1)(x + 1) = 0
x = -1
Titik potong (-1, 0)
Setelah mengetahui nialinya, kita coba gambar grafiknya.
Hubungan antara Koefisien dengan Grafik Fungsi Kuadrat
Kita akan mencari tahu hubungan antara koefisien (a, b, dan c) dengan grafik.
Koefisien A
Langsung kita bahas koefisien a atau koefisien kuadrat. Misalnya kita punya y = x² + 1, y = -x² + 1, dan y = ½ x² + 1, maka grafiknya akan seperti pada berikut.
Kesimpulannya :
• Jika a > 0, grafik terbuka ke atas
• Jika a < 0, grafik terbuka ke bawah
• Semakin besar nilai a, bentuk grafik semakin sempit
》Koefisien B
Koefisien B disebut juga koefisien linear. Langsung saja, misalnya kita punya contoh persamaan y = x² + 2x + 4.
Kemudian, bentuk tersebut jika dilengkapi kuadrat sempurnanya akan menjadi (x + 1)² + 5, selanjutnya 1 kita sebut c dan 5 kita sebut d. Sebelumnya perlu kamu ketahui dulu tentang ini.
• Jika c positif, maka sumbu simetri x = -c, titik puncak (-c, d)
• Jika c negatif, maka sumbu simetri x = c, titik puncak (c, d)
Kira-kira, grafiknya akan seperti berikut.
》Konstanta C
Konstanta c berpengaruh pada titik potong sumbu y.
• Jika c semakin besar, semakin berada di atas
• Jika c semakin kecil, semakin berada di bawah
Perhatikan grafik di bawah
》Hubungan antara Diskriminan dengan Grafik Fungsi Kuadrat
Diskriminan adalah nilai yang dapat digunakan untuk menentukan banyaknya solusi persamaan kuadrat.
• Jika D > 0, akan ada 2 solusi real, atau grafik akan 2 kali menyentuh sumbu x.
• Jika D = 0, akan ada 1 solusi real, atau grafik akan sekali menyentuh sumbu x.
• Jika D < 0, tidak ada solusi real, atau grafik tidak akan menyentuh sumbu x.
○ Contohnya kita punya fungsi y = 3x² + x + 1, berapa nilai diskriminannya?
D = b² – 4ac = 1² – 4(3)(1)= -11, berarti nilai D < 0, maka grafiknya seperti berikut.







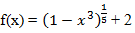
Komentar
Posting Komentar